PULSE: Peeling-based Ultra-Low complexity algorithms for Sparse signal Estimation

An emerging challenge in recent years for engineers, researchers, and data scientists across the globe is to acquire, store, and analyze ever-increasing amounts of data. In the past decade, a new paradigm in data acquisition called “compressed-sensing” has emerged to cope with this data explosion. Compressed sensing exploits the fact that in many applications, although the signal of interest has a large ambient dimension, the relevant information resides in a significantly lower dimensional space. For example, the Magnetic-Resonance-Imaging (MRI) data is sparse in the wavelet-domain. In this project, we consider the problem of computing a sparse Discrete-Fourier-Transform of a high-dimensional signal from its time-domain samples, as a representative example of compressed-sensing problems. We use this problem to investigate the tradeoff between the number of measurements, noise robustness, and the computational complexity of the recovery algorithm in compressed sensing problems.

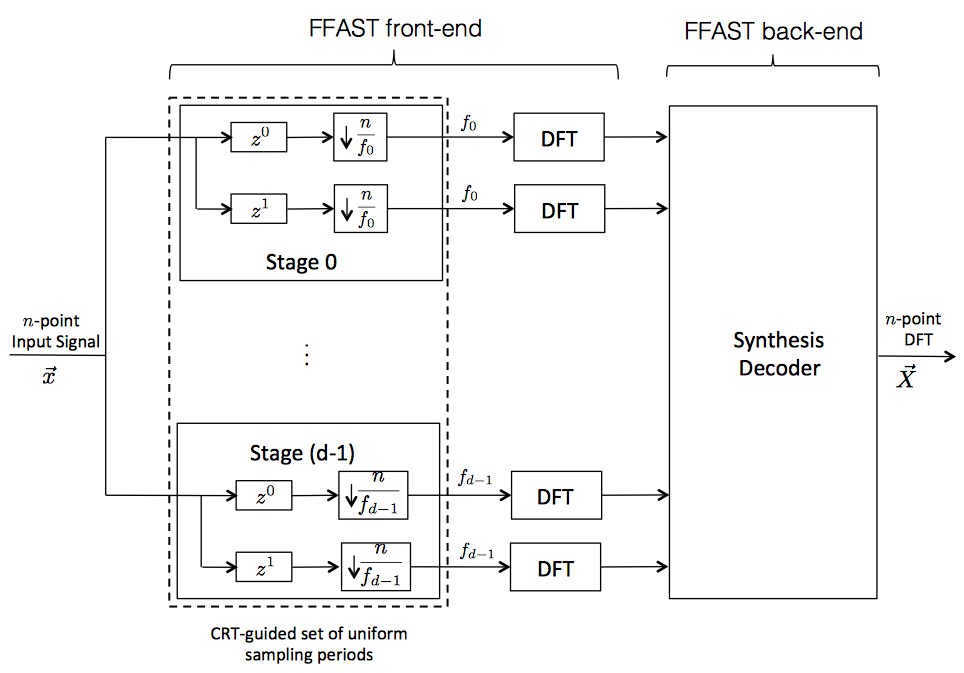
We propose a new family of deterministic sparse sensing matrices, obtained by blending together diverse ideas from sparse graph codes, digital signal processing, and number-theoretic concepts like the Chinese-remainder-theorem (CRT). The specific sparse structure of the proposed family of measurement matrices further enables a Peeling-based Ultra-Low complexity algorithms for Sparse signal Estimation, that are accordingly dubbed PULSE algorithms. Further, using the CRT, we establish an intimate connection between the problem of computing a sparse DFT of a signal and decoding over an appropriately designed sparse graph code. This connection is then exploited 1) to design a sample efficient measurement matrix and a low-complexity peeling-style iterative recovery algorithm, and 2) to perform a rigorous analysis of the recovery algorithm by wielding powerful and well-established analytical tools like density-evolution, martingales, and expander graphs from the coding theory literature. In particular, we show that under some mild conditions a k-sparse n-length DFT of a signal can be computed using (nearly optimal) 4k measurements and O(k log k) computations. As a concrete example, when k = 300, and n = 3.8 × 106, our algorithm achieves computational savings by a factor of more than 6000, and savings in the number of input samples by a factor of more than 3900 over the standard Fast-Fourier-Transform(FFT) algorithms. This can be a significant advantage in many existing applications and can enable new classes of applications that were not thought to be practical so far. Next, we extend these results to the case of noise-corrupted samples, computing sparse 2D-DFTs as well as to interpolation of multi-variate sparse polynomials over the complex field and finite fields. We also demonstrate an application of the proposed PULSE algorithm to acquire the Magnetic-Resonance-Imaging of the Brain. This provides some empirical evidence that PULSE algorithms are applicable for acquiring more realistic signals. The proposed sensing framework and the recovery algorithm are sample efficient and robust against observation noise. We believe that this framework provides a possible direction towards designing efficient and low-power engineering solutions for sparse signal acquisition.

Publications

1. S. Pawar, K. Ramchandran, “Computing a k-sparse n-length Discrete Fourier Transform using at most 4k samples and O(k log k) complexity”, ISIT 2013, Istanbul, Turkey.

2. S. Pawar, K. Ramchandran, “A robust FFAST framework for computing a k-sparse n-length DFT in O(k log n) sample complexity using sparse-graph codes”, (ISIT-2014 extended version) pdf

3. X. Li, J.K. Bradley, S. Pawar, K. Ramchandran, “Robustifying the Sparse Walsh-Hadamard Transform without Increasing the Sample Complexity of O(K log N)”, Technical Report, full version of our submission to ISIT 2014 with the same title. pdf